偏光素子(ジョーンズ行列)

July 09, 2022

偏光子や波長板による偏光状態の変更はジョーンズ行列 $J$ によって一般に、

\begin{aligned} \begin{pmatrix} E_x^{'} \\ E_y^{'} \\ \end{pmatrix} =J \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \end{aligned}

と表せます。

回転行列

最初に回転行列だけ定義しておきます。 $x,y$ 軸上の点を $\theta$ 回転させるには、回転行列 $R$ を用いて、

\begin{aligned} \begin{pmatrix} x^{'} \\ y^{'} \\ \end{pmatrix} &=R(\theta) \begin{pmatrix} x \\ y \\ \end{pmatrix} \\ &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix} \end{aligned}

と表せます。よって電場も同じく、

\begin{aligned} \begin{pmatrix} E_x^{'} \\ E_y^{'} \\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \end{aligned}

となります。

偏光子、検光子

偏光子を通る光は透過軸に沿った直線変更になるため、透過軸が、 $x$ 軸のみ透過させる行列

\begin{aligned} T= \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ \end{pmatrix} \end{aligned}

を用いて、

\begin{aligned} E^{'}&=R(\theta)TR(\theta)^{-1}E \\ \begin{pmatrix} E_x^{'} \\ E_y^{'} \\ \end{pmatrix} &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \\ &= \begin{pmatrix} \cos^2 \theta & \sin \theta \cos \theta \\ \sin \theta \cos \theta & \sin^2 \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \\ &= \begin{pmatrix} \cos^2 \theta & \dfrac{1}{2} \sin (2\theta) \\ \dfrac{1}{2} \sin (2\theta) & \sin^2 \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \end{aligned}

と表すことが出来ます。 $R(\theta)^{-1}$ は $R(\theta)$ の逆回転です。よって $x$ 軸から右回りに $\theta$ 回転した偏光子のジョーンズ行列 $T_\theta$ は

\begin{aligned} T_\theta= \begin{pmatrix} \cos^2 \theta & \dfrac{1}{2} \sin (2\theta) \\ \dfrac{1}{2} \sin (2\theta) & \sin^2 \theta \\ \end{pmatrix} \end{aligned}

となります。 Pythonで実装してみます。x軸方向に偏向面をもつ電場を用意して、検光子の角度を変えて、通り抜けてきた光の強度をプロットしてみます。

E_in = np.array([1, 0]).reshape([-1,1]) * np.exp(1.0j) # 電場の列ベクトル

theta = np.linspace(-np.pi, np.pi, 100) # 検光子の角度

T_theta = np.array([[np.cos(theta)**2, np.sin(2*theta)/2],
                    [np.sin(2*theta)/2, np.sin(theta)**2]]) # 検光子のジョーンズ行列

E_out = []
for i in range(len(theta)):
    E_out.append(T_theta[:,:,i] @ E_in) # 各角度ごとにジョーンズ行列をE_inに作用

E_out = np.array(E_out)
I = np.abs(E_out[:, 0, 0]) **2 + np.abs(E_out[:, 1, 0])**2 # 電場から光強度へ

# プロット
plt.plot(theta, I)
plt.xticks(np.arange(-np.pi, np.pi+0.1, np.pi/2), [r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"])
plt.xlabel("$\\theta$")
plt.ylabel("Intensity")
plt.show()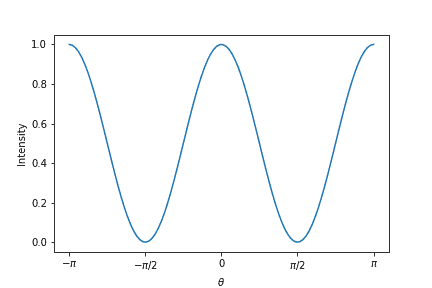

$\theta=0$ で最大となり、偏向面と直角になる $\theta=\pi/2$ で光強度が0となることがわかります。

波長板

$x$ 軸にfast軸をもつ波長板に置いて、位相を $\delta$ だけ進める行列 $M$ は

\begin{aligned} M= \begin{pmatrix} e^{i\dfrac{\delta}{2}} & 0 \\ 0 & e^{-i\dfrac{\delta}{2}} \\ \end{pmatrix} \end{aligned}

として表せます。この波長板が $x$ 軸から $\theta$ だけ傾いて入れば、波長板を通過する電場は次のように表せます。

\begin{aligned} E^{'} &= RMR^{-1}E \\ \begin{pmatrix} E_x^{'} \\ E_y^{'} \\ \end{pmatrix} &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} e^{i\dfrac{\delta}{2}} & 0 \\ 0 & e^{-i\dfrac{\delta}{2}} \\ \end{pmatrix} \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \\ &= \begin{pmatrix} e^{i\dfrac{\delta}{2}}\cos^2 \theta + e^{-i\dfrac{\delta}{2}}\sin^2 \theta & i\sin(2\theta) \sin\left( \dfrac{\delta}{2}\right) \\ i\sin(2\theta)\sin\left( \dfrac{\delta}{2}\right) & e^{i\dfrac{\delta}{2}}\sin^2 \theta + e^{-i\dfrac{\delta}{2}}\cos^2 \theta \\ \end{pmatrix} \begin{pmatrix} E_x \\ E_y \\ \end{pmatrix} \end{aligned}

よってfast軸が $x$ 軸から右回りに $\theta$ 傾いて、fast軸を $\delta$ だけ早める波長板のジョーンズ行列は

M_{\theta, \delta} = \begin{pmatrix} e^{i\dfrac{\delta}{2}}\cos^2 \theta + e^{-i\dfrac{\delta}{2}}\sin^2 \theta & i\sin(2\theta) \sin\left( \dfrac{\delta}{2}\right) \\ i\sin(2\theta) \sin\left( \dfrac{\delta}{2}\right) & e^{i\dfrac{\delta}{2}}\sin^2 \theta + e^{-i\dfrac{\delta}{2}}\cos^2 \theta \\ \end{pmatrix}

となります。

参考第 3 章 Jones 法による偏光状態の変換の記述